[ 다이나믹 프로그래밍 ]
다이나믹 프로그래밍(Dynamic Programing)은 메모리를 적절하게 사용하는 방법으로 알고리즘의 수행 시간을 향상시키는 것을 목적으로 둔다. 메모리는 작은 문제라고 불리는 이미 계산된 결과를 저장하는 데 사용된다. 다이나믹 프로그래밍을 구현하는 방법은 탑다운 방식과 바텀업 방식 이렇게 두 가지로 알려져 있다.
결과적으로는 이렇게 작은 문제를 저장해서 이미 계산된 내역을 메모리에서 빠르게 찾아서 문제를 해결한다는 것이다. 이런 문제를 해결할 수 있는 조건이 두가지가 있는데 하나는 최적 구조이고 다른 하나는 중복 구조이다. 최적 구조는 큰 문제를 작은 문제로 쪼개서 처리할 수 있는 구조를 말하고 중복 구조는 같은 문제가 반복적으로 나오는 구조로 볼 수 있다.
대표적인 중복문제는 피보나치 수열 알고리즘이다. 피보나치 수열은 "0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946"라는 값을 가지고 있다. 점화식으로 $a_n = a_{n-1} + a_{n-2}$ 를 사용하는데 이 수식을 파이썬 코드로 확인하고 트리구조로 보면 반복되는 구간이 많다. 재귀함수로 계속 트리를 만들면서 값을 만들고 탈출문인 if문을 만나면서 종료가 되는데 이때 같은 계산과 결과를 가진 가지들이 다수 만들어진다.
순서를 보면 하나도 빠짐없이 계산을 하는데 이때 발생하는 시간 복잡도가 $O(2^n)$ 이다.
def fibo(x):
if x ==1 or x ==2:
return 1
return fibo(x - 1) + fibo(x - 2)
print("결과 : " + str(fibo(6)))
#피보나이 수열은 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377....
> 결과 : 8
> 순서
fibo(6) > fibo(5) > fibo(4) > fibo(3) > fibo(2) > fibo(1) > fibo(2) >
fibo(3) > fibo(2) > fibo(1) > fibo(4) > fibo(3) > fibo(2) > fibo(1) >
fibo(2)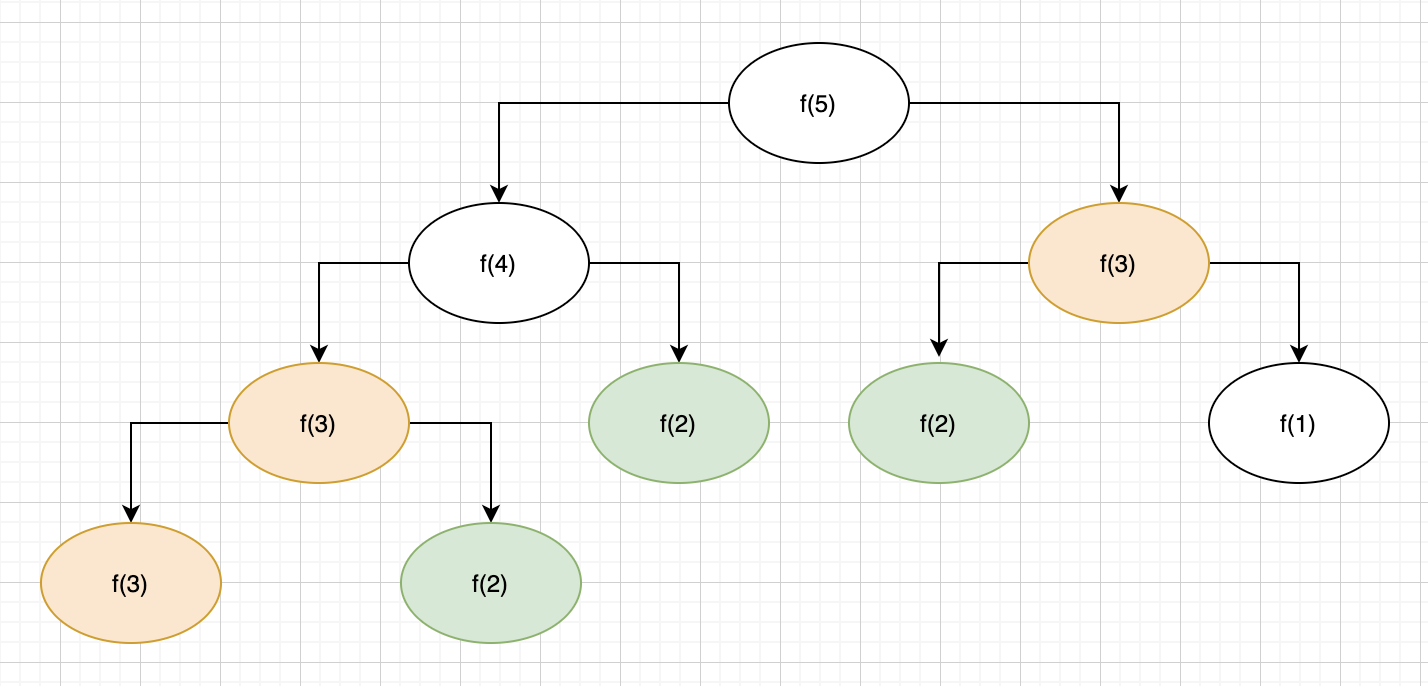
[ 다이나믹 프로그래밍으로 문제 해결 ]
다이나믹 프로그래밍을 사용하는 방식은 탑다운(Top-Down), 바텀업(Bottom-Up) 이렇게 두 가지가 있는데 기본적으로 바텀업을 사용해서 작은 문제를 해결하고 큰 문제까지 해결할 수 있는 방법을 선택한다.
우선 탑다운(하양식) 방식을 알아보겠다. 탑다운은 우선 저장된 값이 있는지 확인해서 값이 있을 경우 갖고 있는 값을 반환하는 구조이다. 이 구조를 메모리제이션(Memorization)이라고 한다.
코드를 보면 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]처럼 0의 값으로 이루어진 d라는 리스트를 만들었다. 이후 1과 2일 경우에는 1을 반환하게 했으며 리스트의 값이 0이 아닌 곳은 이미 계산이 되어 있기 때문에 계산된 값을 반환하게 설정했다.
fibo(6)라는 값을 넣어서 확인해보면 [0, 0, 0, 2, 3, 5, 8, 0, 0, 0]라는 리스트가 만들어진 것을 아 수 있다. index 6에 위치한 값이 8이라는 값으로 잘 넣어진 것을 확인할 수 있다. 이렇게 리스트에 저장해서 저장된 값이 0이 아닌 것을 확인하면서 피보나치 수열 값을 반환하는 다이나믹 프로그래밍을 알아보았다.
d = [0] * 10
def fibo(x):
if x == 1 or x ==2:
return 1
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print("결과 : " + str(fibo(6)))
print(str(d))
#피보나이 수열은 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377....
> 결과 : 8
> [0, 0, 0, 2, 3, 5, 8, 0, 0, 0]
> 순서
fibo(6) > fibo(5) > fibo(4) > fibo(3)
> 시간 복잡도 : O(N)
이제 가장 제너럴하게 사용되고 있는 보텀업(상향식)에 대해서 알아보겠다. 보텀업은 시작 값을 통해서 계산을 시작하고 점차 큰 값을 계산하는 방식으로 볼 수 있다. for문에서는 $a_n = a_{n-1} + a_{n-2}$ 점화식을 그대로 확인할 수 있다.
d = [0] * 10
d[1] = 1
d[2] = 1
n = 8
for i in range(3, n + 1):
d[i] = d[i - 1] + d[i - 2]
print("결과 : " + str(d[6]))
print(d)
> 결과 : 8
> [0, 1, 1, 2, 3, 5, 8, 13, 21, 0]
다이나믹 프로그래밍을 구현하게 될 경우 비약적인 속도를 얻을 수 있으므로 개발할 때 적용 가능한지 확인해서 구현하는 것이 현명한 방법이다.
'동굴 속 정보' 카테고리의 다른 글
| Greedy Algorithm Python (0) | 2021.04.11 |
|---|---|
| 빅오(Big O) 시간복잡도 (0) | 2021.04.10 |
| 최적 알고리즘과, 루프 불변성 (0) | 2021.04.10 |
| 원하는 버전 패키지 yum으로 설치 (0) | 2021.04.06 |
| 빈센조 전여빈의 옷들 좀 보자 (1) | 2021.04.05 |



